In this tutorial we will look into Dijkstra's algorithm for finding a single source shortest path on a weighted directed graph G = (V,E). We will first look at the algorithm itself and will later understand it using a simple example. So let's get started now :
Dijkstra's follows a greedy approach in order to calculate the shortest path. It is more efficient when compared with Bellman-Ford Algorithm. We shall assume that there are no negative weights in the graph. Dijkstra's algorithm maintains a set S of vertices whose final shortest-path weights from the source s have already been determined.
This is how the algorithm works :
1. Algorithm selects a vertex u with the minimum shortest path estimate.
2. Adds the vertex u to the set S.
The above steps are executed repeatedly until it finds the shortest path.
Algorithm : First we will look at two helper functions and then the Dijkstra's algorithm itself.
Dijkstra's follows a greedy approach in order to calculate the shortest path. It is more efficient when compared with Bellman-Ford Algorithm. We shall assume that there are no negative weights in the graph. Dijkstra's algorithm maintains a set S of vertices whose final shortest-path weights from the source s have already been determined.
This is how the algorithm works :
1. Algorithm selects a vertex u with the minimum shortest path estimate.
2. Adds the vertex u to the set S.
The above steps are executed repeatedly until it finds the shortest path.
Algorithm : First we will look at two helper functions and then the Dijkstra's algorithm itself.
This function is the first step of the Dijkstra’s algorithm, here for each vertex we will make shortest path ( Step 2 ) Infinity since we are yet to determine that. And since we do not know the path which we will take to reach target node, we will assign Parent node of each vertex as NIL ( Step 3).
The process of relaxing an edge (u,v) consists of testing whether we can improve the shortest path to v found so far by going through u and, if so, updating d[v] and Pi[v].
Line 1 initializes the values in the usual way as described earlier, and line 2 initializes the set S to empty. Line 3 initializes queue Q to all the vertices of the graph. Each time through the while loop lines 4 - 8, Line 5 extracts a vertex u from the Q and Line 6 adds it to the set S. ( The first time through this loop, u = s) Vertex u, therefore, has the smallest shortest-path estimate of any vertex in V - S. Then, lines 7–8 relax each edge (u,v) leaving u, thus updating the estimate d[v] and the predecessor pi[v] if we can improve the shortest path to v found so far by going through u. Observe that the algorithm never inserts vertices into Q after line 3 and that each vertex is extracted from Q and added to S exactly once, so that the while loop of lines 4–8 iterates exactly |V| times.

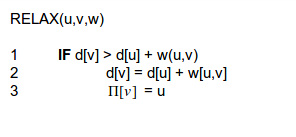



 RSS Feed
RSS Feed